장철원, 『몬테카를로 시뮬레이션으로 배우는 확률통계 with 파이썬 기초 개념부터 확률 과정 기반 데이터 예측까지』, 비제이퍼블릭(2023), p101-182.
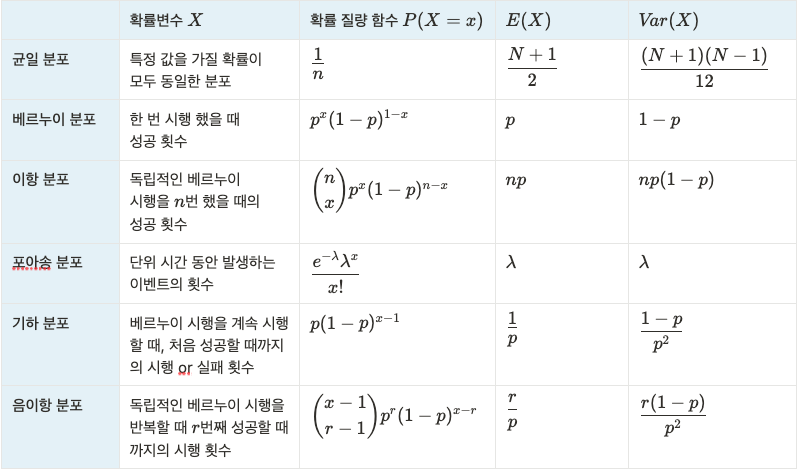
이산형 균일 분포(discrete uniform distribution)
- 균일 분포(uniform distribution): 확률 변수가 특정 값을 가질 확률이 모두 동일한 분포
- 표본 공간이 1부터 시작하는 분포
- \(X\sim U(1, N)\)
- \(P(X=x) = \displaystyle{1\over n}, \;\; x=1,2,\cdots, N\)
- \(\sum^N_{x=1}P(X=x) = 1\) → 확률 질량 함수의 성질
- \(E(X) = \displaystyle{{N+1}\over 2}\)
$$\begin{align*} E(X) & = \displaystyle\sum_xx\cdot f_X(x)\\ & = \sum^N_{x=1}x\cdot {1\over n} \\ & = {1\over N}\sum^N_{x=1}x \\ & = {1\over N}\cdot {{N(N+1)}\over 2} \\ & = {{N+1}\over 2} \end{align*} $$ - \(Var(X) = \displaystyle{{(N+1)(N-1)}\over 12}\)
$$ \begin{align*} E(X^2) & = \sum_xx^2\cdot f_X(x)\\ & =\sum^N_{x=1}x^2\cdot {1\over N} \\ & ={1\over N}\sum^N_{x=1}x^2 \\ & ={1\over N}\cdot {{N(N+1)(2N+1)}\over 6} \\ & = {{(N+1)(2N+1)}\over 6} \end{align*} $$
$$ \begin{align*} Var(X) & = E(X^2) - [E(X)]^2\\ & ={{(N+1)(2N+1)}\over 6} - [{{N+1}\over 2}]^2 \\ & = {{(N+1)(N-1)}\over 12} \end{align*}$$
- 표본 공간이 a와 b 사이의 분포
- \(X\sim U(a, b)\)
- \(P(X=x) = \displaystyle{1\over {b-a+1}}, \;\; x=a,a+1,\cdots, b\)
- \(\sum^b_{x=a}P(X=x) = 1\)
- \(E(X) = \displaystyle{{a+b}\over 2}\)
- \(Var(X) = \displaystyle{{(N+1)(N-1)}\over 12}\)
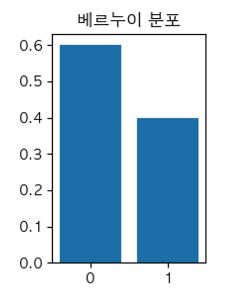
베르누이 분포(Bernoulli distribution)
- 확률 변수 \(X\)는 한 번 시행했을 때 성공 횟수를 의미
- 한 번 시행하기 때문에 베르누이 분포를 베르누이 시행(Bernoulli trial)이라고도 부름
- 베르누이 분포는 한 번 시행했을 때 성공 or 실패 확률을 나타냄
- 확률 질량 함수
- \(X\sim Bernoulli(p)\)
- \(P(X=x)=p^x(1-p)^{1-x}, \;\; x=0, 1\)
- \(\displaystyle\sum^1_{x=0}{P(X=x)} = \sum^1_{x=0}{p^x(1-p)^{1-x}}=(1-p) + p=1\)
- \(E(X)=p\)
$$ \begin{align*} E(X) & = \displaystyle\sum_xx\cdot f_X(x)\\ & = 0\cdot f_X(x) + 1\cdot f_X(x)\\ & = 0\cdot p^0(1-p)^{1-0} + 1\cdot p^1(1-p)^{1-1}\\ & = p \end{align*} $$ - \(Var(X)=p(1-p)\)
$$ \begin{align*} Var(X) & = E[(X-\mu)^2]\\ & = \displaystyle\sum_x{(x-\mu)}^2f_X(x)\\ & = (0-p)^2p^0(1-p)^{1-0} + (1-p)^2p^1(1-p)^{1-1}\\ & = p(1-p) \end{align*} $$
이항 분포(binomial distribution)
- 확률 변수 \(X\)는 독립적인 베르누이 시행을 \(n\)번 했을 때의 성공 횟수를 의미
- \(iid\)를 만족하는 확률 변수 \(Y_1, Y_2, \cdots, Y_n\)이 성공 확률이 \(p\)인 베르누이 분포를 따를 때, 이들의 합인 확률 변수 \(X\)는 이항 분포를 따르는 것
- \(Y_1, Y_2, \cdots, Y_n\sim Bernoulli(p)\)
- \(X=\displaystyle\sum^n_{i=1}Y_i\)
- 확률 질량 함수
- \(X\sim Binomial(n,p)\)
- \(P(X=x) = \dbinom{n}{x}p^x(1-p)^{n-x}, \;\; x=0,1,\cdots ,n\)
- \(\dbinom{n}{x} = \displaystyle{n!\over {x!(n-x)!}}\)
- \(\displaystyle\sum^n_{x=0}{P(X=x)} = \sum^n_{x=0}\dbinom{n}{x}p^x(1-p)^{n-x}=(p+1-p)^n=1\)
- 이항 정리(binomial theorem): \((a+b)^n = \displaystyle\sum^n_{r=0}\dbinom{n}{r}a^rb^{n-r}\)
- 적률 생성 함수
- \(M_x(t) = [pe^t+(1-p)]^n\)
$$ \begin{align*} M_X(t) & = E(e^{tx})\\ & = \displaystyle\sum{e^{tx}\cdot P(X=x)}\\ & = \sum^n_{x=0}{e^{tx}\dbinom{n}{x}p^x(1-p)^{n-x}}\\ & = \sum^n_{x=0}{\dbinom{n}{x}{(pe^t)}^x(1-p)^{n-x}}\\ & = [pe^t + 1-p]^n \end{align*} $$
- \(M_x(t) = [pe^t+(1-p)]^n\)
- \(E(X)=np\)
- 확률 질량 함수
$$ \begin{align*} E(X) & = \displaystyle\sum_x{x\cdot f_X(x)}\\ & = \sum^n_{x=0}{x\dbinom{n}{x}p^x(1-p)^{n-x}}\\ & = \sum^n_{x=1}{x\dbinom{n}{x}p^x(1-p)^{n-x}}\\ & = \sum^n_{x=1}{n\dbinom{n-1}{x-1}p^x(1-p)^{n-x}},\;\; \small x\dbinom{n}{x} = n\dbinom{n-1}{x-1}\\ & = \sum^n_{y=0}{n\dbinom{n-1}{y}p^{y+1}(1-p)^{n-(y+1)}}, \;\;\small y=x-1\\ & = np\sum^{n-1}_{y=0}{\dbinom{n-1}{y}p^{y}(1-p)^{n-(y+1)}}\\ & = np \end{align*} $$ - 적률 생성 함수
$$ \begin{align*} & M_x(t) = [pe^t+(1-p)]^n\\ & M'_X(t) = {d\over dt}M_X(t) = n[pe^t+(1-p)]^{n-1}\cdot pe^t\\ & E(X) = M'_X(0)=n(p+1-p)^{n-1}\cdot p = np \end{align*} $$
- 확률 질량 함수
- \(Var(X) = np(1-p)\)
- 확률 질량 함수
$$ \begin{align*} & Var(X) = E[(X-\mu)^2]=E(X^2)-[E(X)]^2\\ \end{align*} $$
$$ \begin{align*} E(X^2) & = \displaystyle\sum_x{x^2\cdot f_X(x)}\\ & = \sum^n_{x=0}{x^2\dbinom{n}{x}p^x(1-p)^{n-x}}\\ & = \sum^n_{x=1}{xn\dbinom{n-1}{x-1}p^x(1-p)^{n-x}},\;\; \small x\dbinom{n}{x} = n\dbinom{n-1}{x-1}\\ & = n\sum^n_{y=0}{(y+1)\dbinom{n-1}{y}p^{y+1}(1-p)^{n-(y+1)}}, \;\;\small y=x-1\\ & = np\sum^{n-1}{y=0}{y\dbinom{n-1}{y}p^{y}(1-p)^{n-(y+1)}} + np\sum^{n-1}{y=0}{\dbinom{n-1}{y}p^{y}(1-p)^{n-(y+1)}}\\ & = n(n-1)p^2 + np, \;\; \scriptsize np\sum^{n-1}_{y=0}{y\dbinom{n-1}{y}p^{y}(1-p)^{n-(y+1)}} => B(n-1,\; p)의 평균 \end{align*} $$
$$ \begin{align*} Var(X) & = E(X^2)-[E(X)]^2\\ & = n(n-1)p^2 + np -(np)^2\\ & = np(1-p) \end{align*} $$ - 적률 생성 함수
$$ \begin{align*} & M'_X(t) = {d\over dt}M_X(t) = npe^t[pe^t+(1-p)]^{n-1}\\ & M''_X(t) = {d\over dt}M'_X(t) = n(n-1)[pe^t+(1-p)]^{n-2}(pe^t)^2 + npe^t+(1-p)\\ & M''_X(0) = n(n-1)p^2 + np\\ & Var(X) = M''_X(0) - M'_X(0)^2 = n(n-1)p^2 + np - (np)^2 = np(1-p) \end{align*} $$
- 확률 질량 함수
포아송 분포(Poisson distribution)
- 확률 변수 \(X\)는 단위 시간 동안 발생하는 이벤트의 횟수
- 확률 질량 함수
- \(X\sim Poisson(\lambda)\)
- \(P(X=x)=\displaystyle{{e^{-\lambda}\lambda^x}\over x!}, \;\; x=0,1,2,\cdots\)
- \(\displaystyle\sum^\infty_{x=0}P(X=x) = \sum^\infty_{x=0}{{e^{-\lambda}\lambda^x}\over x!}=e^{-\lambda}\sum^\infty_{x=0}{{\lambda^x}\over x!}=e^{-\lambda}e^{\lambda} = 1\)
- \(e^\lambda = \displaystyle\sum^\infty_{x=0}{\lambda^x\over x!}\)
- 테일러 급수: \(f(x) = \displaystyle\sum^\infty_{n=0}{1\over n!}(x-a)^nf^{(n)}(a)\)
- \(f(x) = e^x \;=>\; f'(x)=f''(x)=\cdots=f^{(n)}(x) = e^x\)
- \(e^x = \displaystyle 1 + x + {x^2\over 2!}+ {x^3\over 3!}+ \cdots = \sum^\infty_{n=0}{x^n\over n!}, \;\;a=0\)
- 적률 생성 함수
- \(M_x(t) = e^{\lambda(e^t-1)}\)
$$ \begin{align*} M_X(t) & = E(e^{tx})\\ & = \displaystyle\sum{e^{tx}\cdot P(X=x)}\\ & = \sum^\infty_{x=0}{e^{tx}\cdot {{e^{-\lambda}\lambda^x}\over x!}}\\ & = e^{-\lambda}\sum^\infty_{x=0}{(e^t\lambda)^x\over x!}\\ & = e^{-\lambda}e^{\lambda e^t}\\ & = e^{\lambda(e^t-1)} \end{align*} $$
- \(M_x(t) = e^{\lambda(e^t-1)}\)
- \(E(X)=\lambda\)
- 확률 질량 함수
$$ \begin{align*} E(X) & = \displaystyle\sum_x{x\cdot f_X(x)}\\ & = \sum^\infty_{x=0}{x\cdot {{e^{-\lambda}\lambda^x}\over x!}}\\ & = \sum^\infty_{x=1}{x\cdot {{e^{-\lambda}\lambda^x}\over x!}}\\ & = \lambda e^{-\lambda}\sum^\infty_{x=1}{{\lambda^{x-1}\over (x-1)!}}\\ & = \lambda e^{-\lambda}\sum^\infty_{y=0}{{\lambda^y\over y!}},\;\; \small y=x-1\\ & = \lambda e^{-\lambda}e^{\lambda}\\ & = \lambda \end{align*} $$ - 적률 생성 함수
$$ \begin{align*} & M_x(t) = e^{\lambda(e^t-1)}\\ & M'_X(t) = {d\over dt}M_X(t) = e^{\lambda(e^t-1)}\cdot \lambda e^t\\ & E(X) = M'_X(0)=1\cdot \lambda \cdot 1 = \lambda \end{align*} $$
- 확률 질량 함수
- \(Var(X) = \lambda\)
- 확률 질량 함수
$$ \begin{align*} & Var(X) = E[(X-\mu)^2]=E(X^2)-[E(X)]^2\\ \end{align*} $$
$$ \begin{align*} E(X^2) & = \displaystyle\sum_x{x^2\cdot f_X(x)}\\ & = \sum^n_{x=0}{x^2\cdot{{e^{-\lambda}\lambda^x}\over x!}}\\ & = \sum^n_{x=1}{x^2\cdot{{e^{-\lambda}\lambda^x}\over x!}}\\ & = \lambda e^{-\lambda}\sum^n_{x=1}{x^2\cdot{{\lambda^{x-1}}\over x!}}\\ & = \lambda e^{-\lambda}\sum^n_{x=1} {x\cdot{{\lambda^{x-1}}\over (x-1)!}}\\ & = \lambda e^{-\lambda}\sum^n_{x=1}{(x-1+1)\cdot{{\lambda^{x-1}}\over (x-1)!}}\\ & = \lambda e^{-\lambda}\Big[\sum^n_{x=2}{{{\lambda^{x-2}\lambda}\over (x-2)!} + \sum^n_{x=1}{{\lambda^{x-1}}\over (x-1)!}}\Big]\\ & = \lambda e^{-\lambda}(\lambda e^{\lambda} + e^{\lambda})\\ & = \lambda^2 + \lambda \end{align*} $$
$$ \begin{align*} Var(X) & = E(X^2)-[E(X)]^2\\ & = \lambda^2 + \lambda - \lambda^2\\ & = \lambda \end{align*} $$ - 적률 생성 함수
$$ \begin{align*} & M'_X(t) = {d\over dt}M_X(t) = e^{\lambda(e^t-1)}\cdot \lambda e^t\\ & M''_X(t) = {d\over dt}M'_X(t) = \lambda e^t \cdot e^{\lambda(e^t-1)} + \lambda e^t \cdot e^{\lambda(e^t-1)} \cdot (\lambda e^t),\;\; \small y=e^{f(x)} \to y'=e^{f(x)}f'(x) \\ & M''_X(0) = \lambda + \lambda^2\\ & Var(X) = M''_X(0) - M'_X(0)^2 = \lambda + \lambda^2 - \lambda^2 = \lambda \end{align*} $$
- 확률 질량 함수

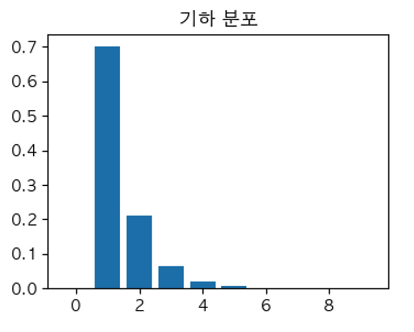
기하 분포(Geometric distribution)
- 확률 변수 \(X\)는 베르누이 시행을 계속 시행할 때, 처음 성공할 때까지의 시행 or 실패 횟수
- \(Y=X-1\), \(Y\): 처음 성공할 때까지의 실패 횟수
- 확률 변수: 시행 횟수
- \(X=처음\;성공할\;때까지의\;시행\;횟수\)
- \(Z_1, Z_2, \cdots,Z_n \sim Bernoulli(p)\)
- \(X=inf\{n:Z_n=1\}\)
- \(X \sim Geometric(p)\)
- 확률 질량 함수
- \(P(X=x)=p(1-p)^{x-1},\;\; \small x=1,2,\cdots\)
$$ \begin{align*} \sum^\infty_{x=1}P(X=x) & = \displaystyle\sum^\infty_{x=1}p(1-p)^{x-1}\\ & = p\sum^\infty_{x=1}(1-p)^{x-1}\\ & = p\cdot{1\over {1-(1-p)}}\\ & = p\cdot {1\over p}\\ & = 1 \end{align*} $$
- \(P(X=x)=p(1-p)^{x-1},\;\; \small x=1,2,\cdots\)
- 확률 변수: 실패 횟수
- \(Y=처음\;성공할\;때까지의\;실패\;횟수\)
- \(Y \sim Geometric(p)\)
- \(X=Y+1\)
- \(Y=X-1\)
- 확률 질량 함수
- \(P(Y=y)=p(1-p)^y,\;\; \small y=0,1,\cdots\)
$$ \begin{align*} \sum^\infty_{y=0}P(Y=y) & = \displaystyle\sum^\infty_{y=0}p(1-p)^y\\ & = p\sum^\infty_{y=0}(1-p)^y\\ & = p\cdot{1\over {1-(1-p)}}\\ & = p\cdot {1\over p}\\ & = 1 \end{align*} $$
- \(P(Y=y)=p(1-p)^y,\;\; \small y=0,1,\cdots\)
- 누적 분포 함수
- \(P(X=x) = p(1-p)^{x-1},\;\; \small x=1,2,\cdots\)
$$ \begin{align*} P(X\le x) & = \displaystyle\sum^x_{k=1}p(1-p)^{k-1}\\ & = p\sum^x_{k=1}(1-p)^{k-1}\\ & = p\cdot{{(1-p)^x-1}\over {(1-p)-1}}\\ & = 1-(1-p)^x \end{align*} $$
$$ \begin{align*} P(X\gt x) & = 1 - P(X\le x)\\ & = 1-[1-(1-p)^x]\\ & = (1-p)^x \end{align*} $$
- \(P(X=x) = p(1-p)^{x-1},\;\; \small x=1,2,\cdots\)
- 적률 생성 함수
- \(M_x(t) = \displaystyle{{pe^t}\over {1-(1-p)e^t}}\)
$$ \begin{align*} M_X(t) & = E(e^{tx})\\ & = \displaystyle\sum{e^{tx}\cdot P(X=x)}\\ & = \sum^\infty_{x=0}{e^{tx}\cdot p(1-p)^{x-1}}\\ & = p\sum^\infty_{x=0}{e^{tx}\cdot (1-p)^x(1-p)^{-1}}\\ & = {p\over {1-p}}\sum^\infty_{x=0}{[e^t(1-p)]^x}\\ & = {p\over {1-p}}\cdot {{e^t(1- p)}\over {1-e^t(1-p)}}\\ & = {{pe^t}\over {1-e^t(1-p)}} \end{align*} $$
- \(M_x(t) = \displaystyle{{pe^t}\over {1-(1-p)e^t}}\)
- 무기억성(memoryless property)
- \(P(X\gt y+z\;|\;X\gt y)=P(X\gt z),\;\; \small for\;all\;y,\;z\gt 0\)
- \(P(X\gt y+z)=P(X\gt y)P(X\gt z),\;\; \small for\;all\;y,\;z\gt 0\)
$$ \begin{align*} P(X\gt y+z\;|\;X\gt y) & = {{P(\{X\gt y+z\}\cap \{X\gt y\})}\over {P(X\gt y)}}\\ & = {P(X\gt y+z)}\over {P(X\gt y)}\\ & = {{(1-p)^{y+z}}\over {(1-p)^y}}\\ & = (1-p)^z\\ & = P(X\gt z) \end{align*} $$
- \(P(X\gt n) = P(X\gt 1)^n\)
- \(P(X\gt y+1)=P(X\gt y)P(X\gt 1)\)
- \(E(X) = \displaystyle{1\over p}\)
- 확률 질량 함수
$$ \begin{align*} E(X) & = \displaystyle\sum_x{x\cdot f_X(x)}\\ & = \sum^\infty_{x=1}{x\cdot p(1-p)^{x-1}}\\ & = p\sum^\infty_{x=1}{x\cdot (1-p)^{x-1}}\\ & = p[1+2(1-p)+3(1-p)^2+\cdots]\\ & = p\cdot {1\over p}[1+(1-p)+(1-p)^2+\cdots]\\ & = \sum^\infty_{x=1}(1-p)^{x-1}\\ & = {1\over {1-(1-p)}}\\ & = {1\over p} \end{align*} $$
$$ \begin{align*} \displaystyle S=1+2(1-p)+3(1-p)^2+\cdots \\ (1-p)S = (1-p) + 2(1-p)^2 + 3(1-p)^3+\cdots \\ \Downarrow \space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\\ S-(1-p)S = 1 + (1-p) + (1-p)^2 + (1-p)^3+\cdots\\ \iff pS = 1 + (1-p) + (1-p)^2 + (1-p)^3+\cdots\\ \iff S = {1\over p}[1 + (1-p) + (1-p)^2 + (1-p)^3+\cdots] \\ \end{align*} $$
- 확률 질량 함수
- \(Var(X) = \displaystyle{{1-p}\over p^2}\)
- 확률 질량 함수
$$ \begin{align*} & Var(X) = E[(X-\mu)^2]=E(X^2)-[E(X)]^2\\ \end{align*} $$
$$ \begin{align*}
E(X^2) & = \displaystyle\sum_x{x^2\cdot f_X(x)}\\
& = \sum^n_{x=1}{x^2\cdot{p(1-p)^{x-1}}}\\
& = p\sum^n_{x=1}{x^2\cdot{(1-p)^{x-1}}}\\
& = p[1(1-p)^{1-1} + 2^2(1-p)^{2-1} + 3^2(1-p)^{3-1}+\cdots]
\end{align*} $$
$$ \begin{align*}
\displaystyle S=1+4(1-p)+9(1-p)^2+\cdots \\
(1-p)S = (1-p) + 4(1-p)^2 + 9(1-p)^3+\cdots \\
\Downarrow \space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\\
S-(1-p)S = 1 + 3(1-p) + 5(1-p)^2 + 7(1-p)^3+\cdots\\
\iff pS = \tiny[2 + 4(1-p) + 6(1-p)^2 + 8(1-p)^3+\cdots] - [1 + (1-p) + (1-p)^2 + (1-p)^3+\cdots]\\
\iff pS = S_2 - S_1 \\
\implies pS = {2\over p^2} - {1\over p} \\
\implies pS = {{2-p}\over p^2}\\
\therefore S = {{2-p}\over p^3},\;\; E(X^2) = {{2-p}\over p^2}
\end{align*} $$
$$ \begin{align*}
S_1 & = 1 + (1-p) + (1-p)^2 + \cdots\\
& = \sum^\infty_{x=1}(1-p)^{x-1}\\
& = {1\over {1-(1-p)}}\\
& = {1\over p}
\end{align*} $$
$$ \begin{align*}
\displaystyle S_2=2+4(1-p)+6(1-p)^2+\cdots \\
(1-p)S_2 = 2(1-p) + 4(1-p)^2 + 6(1-p)^3+\cdots \\
\Downarrow \space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\\
S_2-(1-p)S_2 = 2 + 2(1-p) + 2(1-p)^2 + 2(1-p)^3+\cdots\\
\implies pS_2 = \sum^\infty_{x=1}{2(1-p)^{x-1}}\\
\implies pS_2 = {2\over {1-(1-p)}}\\
\implies pS_2 = {2\over p} \\
\therefore S_2 = {2\over p^2}
\end{align*} $$
$$ \begin{align*}
Var(X) & = E(X^2)-[E(X)]^2\\
& = {{2-p}\over p^2} - ({1\over p})^2\\
& = {{1-p}\over p^2}
\end{align*} $$
- 확률 질량 함수
음이항 분포(Negative Binomial distribution)
- 확률 변수 \(X\)는 독립적인 베르누이 시행을 반복할 때 \(r\)번째 성공할 때까지의 시행 횟수
- 확률 변수: 성공할 때까지의 시행 횟수
- \(X=r번\;성공할\;때까지의\;시행\;횟수\)
- \(Z_1, Z_2, \cdots,Z_n \sim Bernoulli(p)\)
- \(X=inf\{n:\displaystyle\sum^n_{i=1}Z_i=r\}\)
- \(X \sim NegativeBinomial(p)\)
- 확률 질량 함수
- \(P(X=x)=\dbinom{x-1}{r-1}p^r(1-p)^{x-r},\;\; \small x=r,r+1,\cdots\)
- 확률 변수: 성공할 때까지의 실패 횟수
- \(Y=r번\;성공할\;때까지의\;실패\;횟수\)
- \(Y \sim NegativeBinomial(p)\)
- \(X=Y+r\)
- \(Y=X-r\)
- 확률 질량 함수
- \(P(Y=y)=\dbinom{r+y-1}{y}p^r(1-p)^y,\;\; \small y=0,1,\cdots\)
- 음이항 분포와 기하 분포의 관계
- 기하 분포: 첫 번째 성공까지의 시행/실패 횟수
- 음이항 분포: r번째 성공까지의 시행/실패 횟수
$$ \begin{align*}
X_r=X_1 + (X_2-X_1)+(X_3+X_2)+\cdots+(X_r-X_{r-1})\\ X_1\sim Geometric(p)\\ X_2-X_1\sim Geometric(p)\\ \vdots\\ X_r-X_{r-1}\sim Geometric(p)\\
\end{align*} $$
- \(E(X) = \displaystyle{r\over p}\)
$$ \begin{align*} E(Y) & = \displaystyle\sum_y{y\cdot f_Y(y)}\\ & = \sum^\infty_{y=0}{y\cdot \dbinom{r+y-1}{y}p^r(1-p)^y}\\ & = \sum^\infty_{y=1}{y\cdot \dbinom{r+y-1}{y}p^r(1-p)^y}\\ & = \sum^\infty_{y=1}{y{{(r+y-1)!}\over {y!(r+y-1-y)!}}p^r(1-p)^y}\\ & = \sum^\infty_{y=1}{{{(r+y-1)!}\over {(y-1)!({\large r!\over r})}}p^r(1-p)^y}\\ & = r\sum^\infty_{y=1}{{{(r+y-1)!}\over {(y-1)!r!}}p^r(1-p)^y}\\ & = r\sum^\infty_{y=1}{\dbinom{r+y-1}{y-1}p^r(1-p)^y}\\ & = r\sum^\infty_{z=0}{\dbinom{q+z-1}{z}p^{q-1}(1-p)^{z+1}},\;\; \small z=y-1, \;q=r+1\\ & = {r(1-p)\over p}\sum^\infty_{z=0}{\dbinom{q+z-1}{z}p^q(1-p)^z}\\ & = {r(1-p)\over p} \end{align*} $$ - \(Var(X) = \displaystyle{r({1-p})\over p^2}\)
$$ \begin{align*} & Var(Y) = E[(Y-\mu)^2]=E(Y^2)-[E(Y)]^2\\ \end{align*} $$
$$ \therefore E(Y^2) = E[Y(Y-1)] + E(Y) $$
$$ \begin{align*}
E[Y(Y-1)] & = \displaystyle\sum_yy(y-1)\cdot f_Y(y)\\ & = \sum^\infty_{y=0}y(y-1)\dbinom{r+y-1}{y}p^r(1-p)^y\\ & = \sum^\infty_{y=2}y(y-1)\dbinom{r+y-1}{y}p^r(1-p)^y\\ & = r(r+1)\sum^\infty_{y=2}\dbinom{r+y-1}{y-2}p^r(1-p)^y\\ & = r(r+1)\sum^\infty_{z=0}\dbinom{q+z-1}{z}p^{q-2}(1-p)^{z+2},\;\;\small z=y-2,\;q=r+2\\ & = {r(r+1)(1-p)^2\over p^2}\sum^\infty_{z=0}\dbinom{q+z-1}{z}p^q(1-p)^z\\ & = {r(r+1)(1-p)^2\over p^2}
\end{align*}$$
$$ \begin{align*}
E(Y^2) & = E[Y(Y-1)] + E(Y)\\ & = {r(r+1)(1-p)^2\over p^2} + {r(1-p)\over p}
\end{align*}$$
$$ \begin{align*}
Var(Y) & = E(Y^2)-[E(Y)]^2\\ & = {r(r+1)(1-p)^2\over p^2} + {r(1-p)\over p} - \big[{r(1-p)\over p}\big]^2\\ & = {r(1-p)\over p^2}
\end{align*} $$

정리
Reference
반응형
'Math' 카테고리의 다른 글
| Chapter 5. 연속형 확률 분포 (0) | 2023.05.18 |
|---|---|
| Chapter 3. 확률 (0) | 2023.05.03 |
| Chapter 2. 기초 수학 (0) | 2023.04.29 |



댓글