장철원, 『몬테카를로 시뮬레이션으로 배우는 확률통계 with 파이썬 기초 개념부터 확률 과정 기반 데이터 예측까지』, 비제이퍼블릭(2023), p183-258.
1. 연속형 균일 분포(Continuous uniform distribution)
- 확률 변수 \(X\)는 특정 값을 가질 확률이 모두 동일한 분포
- \(X\sim U(a,b)\)
1-a. 확률 밀도 함수
\(f_X(x) = \displaystyle{1\over {b-a}},\;\; \small x\in [a,b]\)
$$ \begin{align*} \int^b_af_X(x)dx & = \displaystyle\int^b_a{1\over {b-a}}dx\\ & = \Big[{1\over {b-a}}\Big]^b_a\\ & = {b\over {b-a}} - {a\over {b-a}}\\ & = 1 \end{align*} $$
1-b. 기댓값
\(E(X) = \displaystyle{(b+a)\over 2}\)
$$ \begin{align*} E(X) & = \displaystyle\int^\infty_{-\infty}{xf_X(x)dx}\\ & = \int^b_a{x{1\over {b-a}}dx}\\ & = {1\over {b-a}}\int^b_a{xdx}\\ & = {1\over {b-a}}\Big[{1\over 2}x^2\Big]^b_a\\ & = {{b+a}\over 2} \end{align*} $$
1-c. 분산
\(Var(X) = \displaystyle{(b-a)^2\over 12}\)
$$ \begin{align*} Var(X) & = E[(X-\mu)^2]\\ & = E(X^2) - [E(X)]^2\\ \end{align*} $$
$$ \begin{align*} E(X^2) & = \displaystyle\int{x^2f_X(x)dx}\\ & = \int^b_a{x^2\cdot {1\over {b-a}}dx}\\ & = {1\over {b-a}}\int^b_a{x^2dx}\\ & = {1\over {b-a}}\Big[{1\over 3}x^3\Big]^b_a\\ & = {{a^2 + ab + b^2}\over 3} \end{align*} $$
$$ \begin{align*} Var(X) & = E[(X-\mu)^2]\\ & = E(X^2) - [E(X)]^2\\ & = {{a^2 + ab + b^2}\over 3} - ({{b+a}\over 2})^2\\ & = {{(b-a)^2}\over 12} \end{align*} $$
2. 정규 분포(Normal distribution)
- 연속형 확률 분포에서 가장 기본이 되는 분포
- 확률 변수 \(X\)가 정규 분포를 따를 때, 평균 \(\mu\), 분산 \(\sigma^2\)
- 평균: 분포의 위치를 정하는 파라미터 (location parameter)
- 분산: 분포의 평균으로부터 흩어짐 정도를 나타내는 파라미터 (scale parameter)
- 68-95-99 법칙
- 평균을 중심으로 \(\pm1\sigma\): 전체의 68%를 차지
- 평균을 중심으로 \(\pm2\sigma\): 전체의 95%를 차지
- 평균을 중심으로 \(\pm3\sigma\): 전체의 99.7%를 차지
- \(X\sim N(\mu, \sigma^2)\)
2-a. 확률 밀도 함수
\(f_X(x) = \displaystyle{1\over {\sqrt{2\pi}\sigma}}{e^{-{1\over 2}({{x-\mu}\over \sigma})^2}},\;\; \small -\infty \lt x\lt \infty\)
2-b. 표준 정규 분포(standard normal distribution)
- \(X\sim N(0,1)\)
- 확률 밀도 함수: \(f_X(x) = \displaystyle{1\over {\sqrt{2}\sigma}}{e^{-{1\over 2}x^2}},\;\; \small -\infty \lt x\lt \infty\)
- \(E(X) = 0\)
- \(Var(X)=1\)
2-c. 정규 근사(normal approximation)
- 이항 분포의 정규 근사
- \(n\)이 커지면 정규 분포에 근접
- 확률 변수 \(X\)가 \(Binomial(n,p)\)를 따를 때, \(n\)이 커지면 평균이 \(np\), 분산이 \(np(1-p)\)인 정규 분포를 따름
- \(X\sim Binomial(n,p)\)
- \(X\sim N(np,\;np(1-p)),\;\;\small as\;n\to\infty\)
- 포아송 분포의 정규 근사
- \(\lambda\)가 커지면 정규 분포에 근접
- 확률 변수 \(X\)가 \(Poisson(\lambda)\)를 따를 때, \(\lambda\)가 커지면 평균이 \(\lambda\) 분산이 \(\lambda\)인 정규 분포를 따름
- \(X\sim Poisson(\lambda)\)
- \(X\sim N(\lambda, \lambda),\;\;\small as\;n\to\infty\)
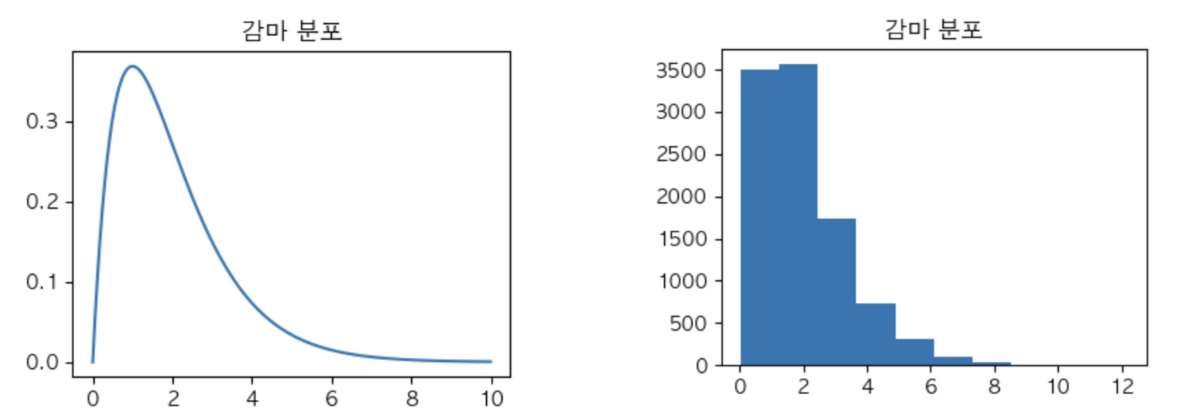
3. 감마 분포(Gamma distribution)
3-a. 감마 함수(gamma function)
- 팩토리얼 함수는 음이 아닌 정수 값만 가질 수 있음 → 불연속 함수
- 감마 함수는 팩토리얼 함수를 연속 함수화 한 것
- \(\Gamma(\alpha) = \int^\infty_0x^{\alpha-1}e^{-x}dx,\;\;\small \alpha>0\)
- 성질
- \(\Gamma(1) = 1\)
$$ \begin{align*} \displaystyle \Gamma(1) & = \int^\infty_0{x^{1-1}e^{-x}dx}, \\ & = \int^\infty_0{e^{-x}dx}\\ & = \big[-e^{-x}\big]^\infty_0\\ & = 1 \end{align*} $$ - \(\Gamma({1\over 2}) = \sqrt\pi\)
$$ \begin{align*} \displaystyle \Gamma\Big({1\over 2}\Big) & = \int^\infty_0{x^{-{1\over 2}}e^{-x}dx} \\ & = \int^\infty_0{u^{-1}e^{-u^2}2u\cdot du},\;\;\small x=u^2 \\ & = \int^\infty_0{x^{-{1\over 2}}e^{-x}dx} \\ & = 2\int^\infty_0{e^{-u^2} du}\\ & = 2\cdot {{\sqrt \pi}\over 2},\;\; \small 가우스\;적분\;활용\\ & = \sqrt \pi \end{align*} $$ - \(\Gamma(\alpha+1) = \alpha\Gamma(\alpha)\)
$$ \begin{align*} \displaystyle \Gamma(\alpha+1) & = \int^\infty_ox^\alpha e^{-x}dx\\ & = \int^\infty_o{\alpha x^{\alpha-1} e^{-x}dx} + \big[-x^\alpha e^{-x}\big]^\infty_0\\ & = \alpha \int^\infty_o{x^{\alpha-1} e^{-x}dx}\\ & = \alpha\Gamma(\alpha) \end{align*} $$ - \(\Gamma(\alpha)=(\alpha-1)!\)
$$ \begin{align*} \displaystyle \Gamma(\alpha) & = (\alpha-1)\Gamma(\alpha-1) \\ & = (\alpha-1)(\alpha-2)\Gamma(\alpha-2) \\ & = (\alpha-1)(\alpha-2)\cdots(1)\Gamma(1) \\ & = (\alpha-1)! \end{align*} $$
- \(\Gamma(1) = 1\)
3-b. 감마 분포
- 확률 변수 \(X\)는 \(\alpha\)번째 성공할 때까지의 대기 시간을 의미
- \(X\sim Gamma(\alpha, \beta)\)
- \(f_X(x)=\displaystyle{1\over {\Gamma(\alpha)\beta^\alpha}}x^{\alpha-1}e^{-{1\over \beta}x},\;\;\small 0\lt x\lt \infty,\;\; \alpha\gt0,\;\;\beta\gt 0\)
- 확률 밀도 함수 증명
$$ \begin{align*} \displaystyle\int^\infty_0f_X(x)dx & = \int^\infty_0{1\over {\Gamma(\alpha)\beta^\alpha}}x^{\alpha-1}e^{-{1\over \beta}x}dx\\ & = {1\over {\Gamma(\alpha)\beta^\alpha}}\int^\infty_0x^{\alpha-1}e^{-{1\over \beta}x}dx\\ & = {1\over {\Gamma(\alpha)\beta^\alpha}}\int^\infty_0{(\beta t)}^{\alpha-1}e^{-t}\beta dt, \;\;\small t={1\over \beta}x,\;\;dt={1\over \beta}dx\\ & = {1\over {\Gamma(\alpha)\beta^\alpha}}\beta^\alpha\int^\infty_0{t}^{\alpha-1}e^{-t}dt\\ & = {1\over {\Gamma(\alpha)\beta^\alpha}}\beta^\alpha \Gamma(\alpha)\\ & = 1 \end{align*} $$ - \(E(X) = \alpha \beta\)
- \(Var(X) = \alpha \beta^2\)
3-c. 적률 생성 함수
- \(M_X(t) = (1-\beta t)^{-\alpha}\)
$$ \begin{align*} \displaystyle M_X(t) & = E(e^{tx})\\ & = \int e^{tx}f_X(x)dx\\ & = \int^\infty_0e^{tx}{1\over {\Gamma(\alpha)\beta^\alpha}}x^{\alpha-1}e^{-{1\over \beta}x}dx\\ & = {1\over {\Gamma(\alpha)\beta^\alpha}}\int^\infty_0x^{\alpha-1}e^{-{1\over \beta }x+tx}dx\\ & = {1\over {\Gamma(\alpha)\beta^\alpha}}\int^\infty_0x^{\alpha-1}e^{-{1\over \beta }(1-\beta t)x}dx\\ & = {1\over {\Gamma(\alpha)\beta^\alpha}}\int^\infty_0{\Big({\beta\over {1-\beta t}} y\Big)}^{\alpha-1}e^{-y}{\beta\over {1-\beta t}}dy, \;\;\small y={1\over \beta }(1-\beta t)x\\ & = {1\over {\Gamma(\alpha)\beta^\alpha}}\Big({\beta\over {1-\beta t}}\Big)^\alpha\int^\infty_0{ y}^{\alpha-1}e^{-y}dy\\ & = {1\over {\Gamma(\alpha)\beta^\alpha}}\Big({\beta\over {1-\beta t}}\Big)^\alpha \Gamma(\alpha)\\ & = (1-\beta t)^{-\alpha} \end{align*} $$
3-d. 기댓값
- \(E(X) = \alpha \beta\)
- 확률 밀도 함수
$$ \begin{align*} \displaystyle \int^\infty_0x^{\alpha}e^{-{1\over \beta }x}dx & = \int^\infty_0{(\beta t)^\alpha e^{-t}\beta dt}, \;\;\small {1\over \beta}x = t\\ & = \beta^{\alpha+1}\int^\infty_0{t^\alpha e^{-t}dt}\\ & = \beta^{\alpha+1}\Gamma(\alpha+1) \end{align*} $$
$$ \begin{align*} \displaystyle E(X) & = \int^\infty_{-\infty}xf_X(x)dx\\ & = \int^\infty_0{x\cdot {1\over {\Gamma(\alpha)\beta^\alpha}}x^{\alpha-1}e^{-{1\over \beta}x}dx}\\ & = {1\over {\Gamma(\alpha)\beta^\alpha}}\int^\infty_0x^{\alpha}e^{-{1\over \beta }x}dx\\ & = {1\over {\Gamma(\alpha)\beta^\alpha}}\Gamma(\alpha+1)\beta^{\alpha+1}\\ & = {1\over {\Gamma(\alpha)\beta^\alpha}}\alpha\Gamma(\alpha)\beta^{\alpha+1}\\ & = \alpha \beta \end{align*} $$ - 적률 생성 함수
- \(M_X(t) = (1-\beta t)^{-\alpha}\)
$$ \begin{align*} \displaystyle E(X) & = M'_X(0)\\ & = \alpha \beta \end{align*} $$
3-e. 분산
- \(Var(X) = \alpha \beta^2\)
- \(Var(X) = E[(X-\mu)^2] = E(X^2) - [E(X)]^2\)
- 확률 밀도 함수
$$ \begin{align*} \displaystyle E(X^2) & = \int x^2f_X(x)dx\\ & = \int^\infty_0{x^2\cdot {1\over {\Gamma(\alpha)\beta^\alpha}}x^{\alpha-1}e^{-{1\over \beta}x}dx}\\ & = {1\over {\Gamma(\alpha)\beta^\alpha}}\int^\infty_0x^{\alpha+1}e^{-{1\over \beta }x}dx\\ & = {1\over {\Gamma(\alpha)\beta^\alpha}}\Gamma(\alpha+2)\beta^{\alpha+2}, \;\;\small 치환\;적분\Big({1\over \beta}x=t\Big)\\ & = \alpha(\alpha+1)\beta^2\\ & = \alpha^2\beta^2 + \alpha\beta^2 \end{align*} $$
$$ \begin{align*} \displaystyle Var(X) & = E(X^2) - [E(X)]^2\\ & = \alpha^2\beta^2 + \alpha\beta^2 - (\alpha\beta)^2\\ & = \alpha\beta^2 \end{align*} $$ - 적률 생성 함수
$$ \begin{align*} \displaystyle M''_X(t) & = {d\over dt}M'_X(t)\\ & = {d\over dt}{[\alpha \beta (1-\beta t)^{-\alpha-1}]}\\ & = \alpha \beta (-\alpha-1)(1-\beta t)^{-\alpha-2}(-\beta)\\ & = \alpha(\alpha+1)\beta^2(1-\beta t)^{-\alpha-2} \end{align*} $$
$$ \begin{align*} \displaystyle M''_X(0) & = \alpha(\alpha+1)\beta^2 \end{align*} $$
$$ \begin{align*} \displaystyle Var(X) & = M''_X(0) - M'_X(0)\\ & = \alpha(\alpha+1)\beta^2 - (\alpha \beta)^2\\ & = \alpha \beta^2 \end{align*} $$
4. 지수 분포(Exponential distribution)
- 감마 분포에서 \(\alpha\)가 1인 특수한 경우를 의미
- 확률 변수 \(X\)는 첫 번째 성공할 때까지의 대기 시간
- \(X\sim Exponential(\beta)\)
4-a. 확률 밀도 함수
\(f_X(x) = \displaystyle{1\over \beta}e^{-{1\over \beta}x},\;\;\small x\gt 0\)
$$ \begin{align*} \int^\infty_0f_X(x)dx & = \displaystyle\int^\infty_0{1\over \beta}e^{-{1\over \beta}x}dx\\ & = {1\over \beta}\int^\infty_0e^{-{1\over \beta}x}dx\\ & = 1 \end{align*} $$
4-b. 무기억성
- \(X\sim Exp(\beta)\)
- \(P(X\gt s+t | X\gt t) = P(X\gt s),\;\;\small for\;all\;s,\;t\gt 0\)
- \(P(X\gt s+t) = P(X\gt s)P(X\gt t),\;\;\small for\;all\;s,\;t\gt 0\)
4-c. 적률 생성 함수
\(M_x(t) = (1-\beta t)^{-1}\)
$$ \begin{align*} M_X(t) & = E(e^{tx})\\ & = \int{e^{tx}f_X(x)dx}\\ & = \int^\infty_0{e^{tx}\cdot {1\over \beta}e^{-{1\over \beta}x}dx}\\ & = {1\over \beta}\int^\infty_0{e^{-({{1-\beta t}\over \beta})}dx}\\ & = {1\over \beta}\big[{{-({\beta \over {1-\beta t}})e^{-({{1-\beta t}\over \beta})x}}}\big]^\infty_0\\ & = (1-\beta t)^{-1}
\end{align*} $$
4-d. 기댓값
\(E(X) = \beta\)
- \(E(X) = \displaystyle\int^\infty_\infty{xf_X(x)dx} = \int^\infty_0{x{1\over \beta}e^{-{1\over \beta}x}dx}\)
- 부분 적분
- \( \{f(x)g(x)\}' = f'(x)g(x) + f(x)g'(x) \\ \to f(x)g(x) = \displaystyle\int{f'(x)g(x)} + \int{f(x)g'(x)} \\ \to \displaystyle\int{f(x)g'(x)} = f(x)g(x) - \displaystyle\int{f'(x)g(x)} \)
- \( f(x) = x,\;\;f'(x)=1\to \; g'(x) = \displaystyle{1\over \beta}e^{-{1\over \beta}x},\;\; g(x) = -e^{-{1\over \beta}x} \)
- 확률 밀도 함수
$$ \begin{align*} E(X) & = \displaystyle\int^\infty_\infty{xf_X(x)dx}\\ & = \int^\infty_0{x{1\over \beta}e^{-{1\over \beta}x}dx}\\ & = -xe^{-{1\over \beta}x}\big|^\infty_0 + \int^\infty_0{e^{-{1\over \beta}x}dx}\\ & = \beta\end{align*} $$ - 적률 생성 함수
$$ \begin{align*} E(X) & = M'_X(0)\\
& = \beta \end{align*} $$
$$ \begin{align*} M'_X(t) & = \displaystyle{d\over dt}(1-\beta t)^{-1}\\ & = -(1-\beta t)^{-2}(-\beta)\\ & = \beta(1-\beta t)^{-2}\\ \end{align*} $$
4-e. 분산
- \(Var(X) = \beta^2\)
- \(Var(X) = E[(X-\mu)^2] = E(X^2) - [E(X)]^2\)
- \(E(X^2)\) 부분 적분
- \(f(x) = x^2,\;\;f'(x)=2x\\ g'(x) = \displaystyle{1\over \beta}e^{-{1\over \beta}x},\;\; g(x) = -e^{-{1\over \beta}x}\)
- 확률 밀도 함수
$$ \begin{align*} E(X^2) & = \displaystyle\int^\infty_\infty{x^2f_X(x)dx}\\ & = \int^\infty_0{x^2{1\over \beta}e^{-{1\over \beta}x}dx}\\ & = -x^2e^{-{1\over \beta}x}\big|^\infty_0 + \int^\infty_0{2xe^{-{1\over \beta}x}dx}\\ & = 2\beta \cdot E(X)\\ & = 2\beta^2\end{align*} $$
$$ \begin{align*} Var(X) & = E(X^2) - [E(X)]^2\\ & = 2\beta^2 - \beta^2\\ & = \beta^2\end{align*} $$ - 적률 생성 함수
$$ \begin{align*} E(X^2) & = M''_X(0)\\ & = 2\beta^2 \end{align*} $$
$$ \begin{align*} M''_X(t) & = \displaystyle{d\over dt}\beta(1-\beta t)^{-2}\\ & = -2\beta(1-\beta t)^{-3}(-\beta)\\ & = 2\beta^2(1-\beta t)^{-3}\\ \end{align*} $$
$$ \begin{align*} Var(X) & = E(X^2) - [E(X)]^2\\ & = 2\beta^2 - \beta^2\\ & = \beta^2 \end{align*} $$

5. 카이제곱 분포(Chi-square distribution)
- 감마 분포의 특수한 형태 → 감마 분포에서 \(\alpha=p/2\), \(\beta=2\)인 경우
5-a. 확률 밀도 함수
\(f_X(x) = \displaystyle{1\over {\Gamma({p\over 2})2^{p\over 2}}}x^{{p\over 2}-1}e^{-{1\over 2}x},\;\;\small 0\lt x\lt \infty\)
5-b. 기댓값
\(E(X) = p, \;\;\small \alpha=p/2,\;\beta=2\)
5-c. 분산
\(Var(X) = 2p, \;\;\small \alpha=p/2,\;\beta=2\)

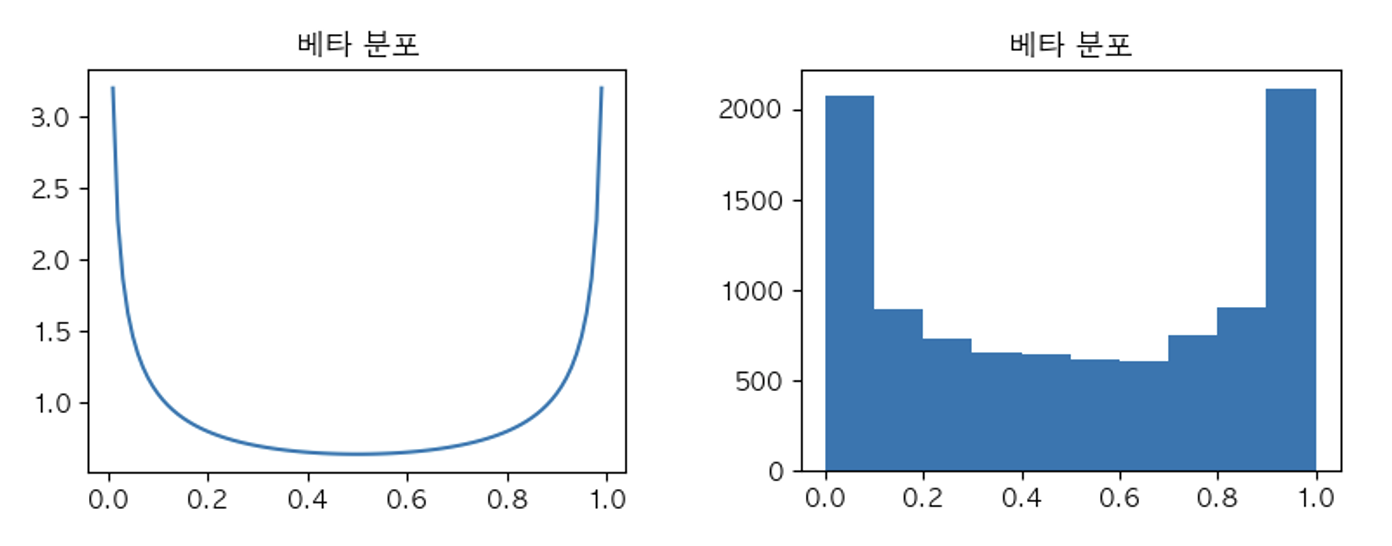
6. 베타 분포(Beta distribution)
6-a. 베타 함수(beta function)
- 이항 계수를 실수 범위로 확장한 것
- \(\rm B(\alpha, \beta) = \displaystyle{{\Gamma{(\alpha)}\Gamma{(\beta)}}\over {\Gamma{(\alpha+\beta)}}}\)
- \(\rm B(\alpha, \beta) = \displaystyle\int^1_0{x^{\alpha-1}(1-x)^{\beta-1}dx}\)
6-b. 확률 밀도 함수
- \(X\sim Beta(\alpha, \beta)\)
- \([0, 1]\)에서 정의 되는 부분은 균일분포와 비슷함
- \(f_X(x) = \displaystyle{{{\Gamma{(\alpha+\beta)}}\over {\Gamma{(\alpha)}\Gamma{(\beta)}}}}{x^{\alpha-1}(1-x)^{\beta-1}},\;\;\small 0\lt x\lt 1, \;\; \alpha\gt 0,\;\;\beta\gt 0\)
$$ \begin{align*} \int^1_0f_X(x)dx & = \int^1_0\displaystyle{{{\Gamma{(\alpha+\beta)}}\over {\Gamma{(\alpha)}\Gamma{(\beta)}}}}{x^{\alpha-1}(1-x)^{\beta-1}}dx\\ & = {{\Gamma{(\alpha+\beta)}}\over {\Gamma{(\alpha)}\Gamma{(\beta)}}}\int^1_0{x^{\alpha-1}(1-x)^{\beta-1}}dx\\
& = {{\Gamma{(\alpha+\beta)}}\over {\Gamma{(\alpha)}\Gamma{(\beta)}}}\cdot {{\Gamma{(\alpha)}\Gamma{(\beta)}}\over {\Gamma{(\alpha+\beta)}}}\\ & = 1 \end{align*} $$
6-c. 기댓값
\(E(X) = \displaystyle{{\alpha}\over {\alpha+\beta}}\)
$$ \begin{align*} \displaystyle E(X) & = \int^\infty_{-\infty}xf_X(x)dx\\ & = \int^1_0{x{{{\Gamma{(\alpha+\beta)}}\over {{\Gamma{(\alpha)}\Gamma{(\beta)}}}}{x^{\alpha-1}(1-x)^{\beta-1}}}dx}\\ & = {{\Gamma{(\alpha+\beta)}}\over {{\Gamma{(\alpha)}\Gamma{(\beta)}}}}\int^1_0{{{x^{\alpha}(1-x)^{\beta-1}}}dx}\\ & = {{\Gamma{(\alpha+\beta)}}\over {{\Gamma{(\alpha)}\Gamma{(\beta)}}}} {\rm B(\alpha+1, \beta)}\\ & = {{\Gamma{(\alpha+\beta)}}\over {{\Gamma{(\alpha)}\Gamma{(\beta)}}}}{{\Gamma{(\alpha+1)}\Gamma{(\beta)}}\over {\Gamma{(\alpha + \beta + 1)}}},\;\;\small \rm B(\alpha, \beta) = \displaystyle{{\Gamma{(\alpha)}\Gamma{(\beta)}}\over {\Gamma{(\alpha+\beta)}}}\\ & = {\alpha \over {\alpha + \beta}},\;\;\small\Gamma(\alpha+1) = \alpha\Gamma(\alpha)\\ \end{align*} $$
6-d. 분산
\(Var(X) = \displaystyle{{\alpha \beta}\over {(\alpha+\beta)^2(\alpha+\beta+1)}}\)
- \(Var(X) = E[(X-\mu)^2] = E(X^2) - [E(X)]^2\)
$$ \begin{align*} E(X^2) & = \displaystyle\int^\infty_\infty{x^2f_X(x)dx}\\ & = \int^1_0{x^2{{{\Gamma{(\alpha+\beta)}}\over {{\Gamma{(\alpha)}\Gamma{(\beta)}}}}{x^{\alpha-1}(1-x)^{\beta-1}}}dx}\\ & = {{\Gamma{(\alpha+\beta)}}\over {{\Gamma{(\alpha)}\Gamma{(\beta)}}}}\int^1_0{{x^{\alpha+1}(1-x)^{\beta-1}}dx}\\ & = {{\Gamma{(\alpha+\beta)}}\over {{\Gamma{(\alpha)}\Gamma{(\beta)}}}}\cdot {{\Gamma{(\alpha+2)}\Gamma{(\beta)}}\over {\Gamma{(\alpha + \beta + 2)}}}\\ & = {{(\alpha+1)\alpha}\over {(\alpha+\beta+1)(\alpha+\beta)}} \end{align*} $$
$$ \begin{align*} Var(X) & = E(X^2) - [E(X)]^2\\ & = {{(\alpha+1)\alpha}\over {(\alpha+\beta+1)(\alpha+\beta)}} - \big({\alpha \over {\alpha + \beta}}\big)^2\\ & = {{\alpha \beta}\over {(\alpha+\beta+1)(\alpha+\beta)^2}} \end{align*} $$
7. 정리

Reference
'Math' 카테고리의 다른 글
| Chapter 4. 이산형 확률 분포 (1) | 2023.05.11 |
|---|---|
| Chapter 3. 확률 (0) | 2023.05.03 |
| Chapter 2. 기초 수학 (0) | 2023.04.29 |



댓글